Library
|
|||||||||||||||
| Print Free Pamphlet - -
Brief Summary Sections :
Introduction
|
|||||||||||||||
|
The Solids named after Plato and Archimedes All of these solids are mathematically associated with √3 In Plato’s Timaeus he explains the world according to geometric shapes. Platonic Solids There are five Platonic solids. They are named for the ancient Greek philosopher Plato who hypothesized in his dialogue, the Timaeus, that the classical elements were made of these regular solids |
|||||||||||||||
|
|||||||||||||||
| Three of the five Platonic Solids use equilateral triangles. |
|||||||||||||||
Plato and The Elements In Plato’s Timaeus he claims that the minute particle of each element had a special geometric shape: tetrahedron (fire), octahedron (air), icosahedron (water), and cube (earth). |
|||||||||||||||
|
|||||||||||||||
| See
Palto’s Timaeus.
|
|||||||||||||||
| The Timaeus makes conjectures on the composition of the four
elements which some ancient Greeks thought constituted the physical
universe: earth, water, air, and fire. Timaeus links each of these
elements to a certain Platonic solid: the element of earth would be a
cube, of air an octahedron, of water an icosahedron, and of fire a
tetrahedron. Each of these perfect polyhedra would
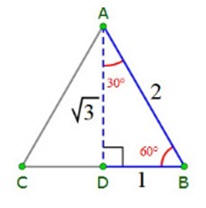
be in turn composed of triangular faces, the 30-60-90 and the
45-45-90 triangles. Each of these perfect polyhedra would be in turn
composed of triangular faces the a 45° - 45° - 90° Δ Triangle and the
30° - 60° - 90° Δ Triangle. These shapes also make extensive use of the
equilateral triangle, 60° - 60° - 60° Δ Triangle. |
|||||||||||||||
|
|
|||||||||||||||
|
See : The Number 153 Was Very Prominent and Recognizable in Ancient Greek Culture |
|||||||||||||||
|
|
|
||||
|
||||
|
||||
|
||||
|
||||